In search of an set of rules is principally regarded as as an very important degree in laptop science that incorporates the use of a step by step process for finding a selected piece of information amongst a big set of information.
With a view to end the process, all seek algorithms make the most of a seek key.
There are various kinds of seek algorithms to be had in laptop science, and the way they’re hired determines the efficiency and potency of the information supplied (the way during which the information is getting used).
Those algorithms are divided into two teams in keeping with the kind of seek operations they carry out.
- Sequential Seek: This system traverses the listing or array consecutively, checking each and every part. (Identical as in terms of a Linear Seek.)
- Period Seek: Those algorithms had been created with the purpose of looking out taken care of information buildings. Some of these seek algorithms are extra environment friendly than Linear Seek as they frequently goal the middle of the hunt construction and divide the hunt area in part. Instance: Binary Seek.
Need a Most sensible Device Construction Task? Get started Right here!
Complete Stack Developer – MERN StackDiscover Program
Forms of Looking Algorithms
- Linear Seek
- Binary Seek
- Leap Seek
- Interpolation Seek
- Exponential Seek
- Sublist Seek (Looking a related listing inside of every other listing)
- Fibonacci Seek
- The Ubiquitous Binary Seek
Linear Seek
A Linear Seek, which could also be popularly referred to as a sequential seek, is a procedure for locating an merchandise in an inventory of things. This kind of looking out set of rules tests each and every part of the listing one after the other till a fit is located or all the listing is searched.
In worst-case eventualities, the Linear Seek takes linear time and plays at maximum n comparisons, the place n is the listing’s period.
If each and every part has an equivalent likelihood of being searched, Linear Seek has a mean case of n+1/2 comparisons, however the reasonable case may also be influenced if the hunt likelihood for each and every part differs. Linear Seek isn’t possible as different seek algorithms and schemes (such because the binary seek set of rules and hash tables) that offer considerably quicker seek operation for all lists.
The next are the stairs taken with enforcing Linear Seek:
- We should first use a for loop to traverse the array components.
- Within the strategy of looking out a component in an inventory of components, we will have to get started via evaluating the hunt part with the present listing of components in each and every iteration of the loop, and if the weather fit, go back the index of the related array part.
- If the part we are in search of does not fit, transfer directly to the following one.
Go back -1, if there is not any fit or the hunt part isn’t discovered within the given array.
What’s Linear Seek in C Programming?
In C, we carry out a Linear Seek to look if a bunch is found in an array. It’s sometimes called sequential seek during which we examine each and every part with the only we are in search of till we discover it or when the listing runs out.
Set of rules of Linear Seek (Manner)
Looking is the process of discovering a undeniable merchandise in an inventory of things. If the part is located within the listing, the method is regarded as a success, and the site of that part is returned; differently, the hunt is regarded as unsuccessful.
In Linear Seek, the index or seek location within the specified array is located. It begins the hunt via evaluating the hunt key to the array/first listing’s part. If the primary part does now not fit the hunt key, the following part will likely be when compared, and so forth till the fit is found out or the array ends. If a fit is found out, the index is returned; differently, it reaches the top of the array or listing, indicating that the hunt key isn’t to be had.
For a greater working out of the Linear seek, we’re going to see an instance.
Instance:
Given array = {50, 90, 30, 70, 60};
Suppose the hunt secret’s 30. Subsequent, scan the array and examine each and every part to the hunt key. The array’s first part is 50, however 50 isn’t equivalent to 30, subsequently proceed directly to the following part. The following part is 90, however it is not equivalent to 30, so it is time to transfer directly to the following one. The array’s subsequent part is 30, which is equal to the hunt key 30, thus returning the index of the array’s present part.
The above instance used to be the case the place the hunt key used to be provide within the array. Now imagine a case the place the hunt key isn’t provide. Let’s think that the hunt key is the same as 10. Examine each and every part within the array with the hunt part. It fails to check with 50, 90, 30, 70, 60, and in the end reaches the array’s conclusion. Because of this, go back -1 or print part isn’t provide within the array, indicating that the hunt key isn’t to be had.
Grasp Core Java 8 Ideas, Java Servlet & Extra!
Java Certification CoachingENROLL NOW
Enforcing C Program for Linear Seek
Code for Linear Seek in C program is given under:
|
#come with <stdio.h> void major() { int num; int i, key, element_found = 0; printf(“Input selection of components you wish to take as enter: “); scanf(“%d”, &num); int arr[num]; printf(“nEnter all of the components of your selection:”); for (i = 0; i < num; i++) { scanf(“%d”, &arr[i]); } printf(“nEnter the important thing part that you simply wish to be searched: “); scanf(“%d”, &key); /* Linear seek begins */ for (i = 0; i < num ; i++) { if (key == arr[i] ) { element_found = 1; damage; } } if (element_found == 1) printf(“we were given the part at index %d”,i+1); else printf(“we haven’t were given part at any index within the arrayn”); } |
Output:
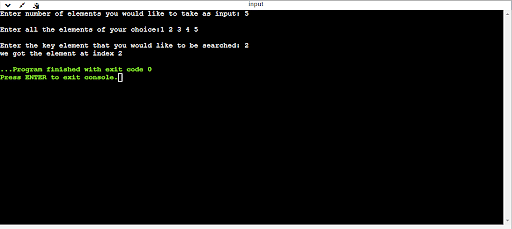
Rationalization of Code:
- In Linear Seek, we search for a component or worth in an array via traversing it from the starting to the top till the specified part or worth is found out.
- The array is searched gradually, and if the important thing part to be searched is located within the array, the location is returned; differently, -1 is returned.
- We’ve not created a serve as specifically for Linear Seek on this C program; as a substitute, we will be able to test for the presence of a component in an array in the principle serve as.
- We traverse the array beginning on the 0th index and lengthening so as of index, breaking the loop there and printing the part’s place within the array, but when the part asked isn’t provide within the array, we merely show “Component isn’t provide within the array.”
- If we had written a separate Linear Seek serve as and the part may now not be discovered within the array, we’d have returned -1 or print “Component isn’t found in array” indicating that the part used to be now not provide.
Linear Seek for More than one Occurrences
The code under prints all of the places the place the wanted part may also be discovered, in addition to the selection of occasions it seems that within the listing of this system.
|
#come with <stdio.h> int major() { int arr[100], key, i, no, depend = 0, seek; printf(“Input selection of components you wish to take as inputn”); scanf(“%d”, &no); printf(“Input %d numbersn”, no); for (i= 0; i < no; i++) scanf(“%d”, &arr[i]); printf(“Input a bunch that you simply wish to searchn”); scanf(“%d”, &seek); for (i = 0; i < no; i++) { if (arr[i] == seek) { printf(“%d is provide at place %d.n”, seek, i+1); depend++; } } if (depend == 0) printf(“%d key isn’t provide within the array.n”, seek); else printf(“%d is provide %d occasions within the array.n”, seek, depend); go back 0; } |
Output:
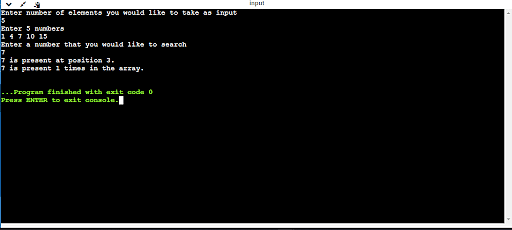
Linear Seek The usage of a Serve as
Code for enforcing Linear Seek in C program via the use of serve as is supplied under:
|
#come with <stdio.h> int linear_search_function(int a[], int n, int key) { for (lengthy i = 0 ;i < n ; i++ ) { if (a[i] == key) go back i; } go back -1; } int major() { int arr[100], key, okay, n, key_position; printf(“Input selection of components within the arrayn”); scanf(“%d”, &n); printf(“Input %d integer(s)n”, n); for (okay= 0; okay < n; okay++) scanf(“%d”, &arr[k]); printf(“Input a bunch you wish to seek within the arrayn”); scanf(“%d”, &key); key_position = linear_search_function(arr, n, key); if (key_position == -1) printf(“%d is not provide within the array.n”, key); else printf(“%d is provide at location %d.n”, key, key_position+1); go back 0; } |
Output:
Need a Most sensible Device Construction Task? Get started Right here!
Complete Stack Developer – MERN StackDiscover Program
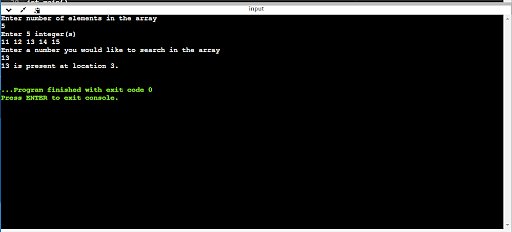
Linear Seek in C The usage of Recursion
The recursive serve as is a serve as that incorporates a decision to itself. Recursion is a technique of defining the recursive serve as. It lets in us to wreck down a large drawback into simply manageable unmarried fundamental scenarios. Divide and overcome could also be an influence and a well-liked laptop programming technique this is broadly used for programming.
|
#come with <stdio.h> int linear_search_with_recursion(int arr[], int worth, int index, int n) { int place = 0; if(index >= n) { go back 0; } else if (arr[index] == worth) { place = index + 1; go back place; } else { go back linear_search_with_recursion(arr, worth, index+1, n); } go back place; } int major() { int n, worth, place, m = 0, arr[100]; printf(“Input the entire components within the array that you simply wish to take:”); scanf(“%d”, &n); printf(“Input the weather of the array:n”); for (int i = 0; i < n; i++) { scanf(“%d”, &arr[i]); } printf(“Input the part you wish to seek within the array: “); scanf(“%d”, &worth); place = linear_search_with_recursion(arr, worth, 0, n); if (place != 0) { printf(“Component discovered at place %d “, place); } else { printf(“Component now not discovered within the array”); } go back 0; } |
Output:
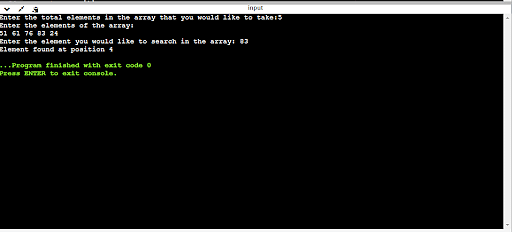
Rationalization of Code:
- In Linear Seek, we search for a component or worth in an array via traversing it from the start till the part or worth we wish is found out.
- The array is searched gradually, and if the important thing part to be searched is located within the array, the location is returned; differently, “Component now not discovered within the array” is outlined.
- On this C program, we have now written a recursive serve as known as linear_search_with_recursion() that takes 4 enter arguments and returns the location of a component in an array that the consumer is looking out.
- If the primary part is located, the index is returned instantly.
- If it’s not the primary member of the array, we scale back the scale of the array via 1 via casting off the primary part, this means that the array measurement will likely be lowered via 1 when Linear Seek-with_recursion() is known as a 2d time (n-1). This will likely proceed till the part has been found out.
Time Complexity of Linear Seek in C Program
The time complexity of an set of rules is not anything however the period of time it takes to run as an algorthm for the entire enter. The selection of operations to be carried out via the set of rules is indicated via the period of enter. On this case, it could now not imagine the set of rules’s total execution time. As an alternative, when the selection of operations in an set of rules will increase or decreases, it’s going to supply information at the variation (build up or aid) in execution time.
Let’s take a look at the complexity of Linear Seek in the appropriate, reasonable, and worst-case eventualities.
Case |
Time Complexity |
|
Very best Case |
O(1) |
|
Moderate Case |
O(n) |
|
Worst case |
O(n) |
- Very best Case Complexity in Linear Seek: In Linear Seek, splendid case happens when the part we are in search of is on the best of the array. The time complexity of Linear Seek within the best-case state of affairs is O (1).
- Moderate Case Complexity: In Linear Seek, the common case time complexity is O(n).
- Worst Case Complexity: The worst case in Linear Seek happens when the part we are searching for for is on the finish of the array. When the objective part isn’t provide within the specified array, the worst-case state of affairs is that we should traverse all the array. The time complexity of Linear Seek within the worst-case state of affairs is O(n).
As a result of each and every member within the array is most effective when compared as soon as, Linear Seek has an O(n) time complexity.
House Complexity of Linear Seek in C Program
In step with their enter measurement, area complexity is largely a dimension of the entire quantity of reminiscence that algorithms or operations require. It’s the quantity of reminiscence area required via the set of rules to resolve a selected example of the computational drawback as a serve as of the enter traits.
As we all know that the quantity of additional information within the Linear Seek is fastened, the gap complexity is at all times O(1).
Boost up your profession as a talented MERN Stack Developer via enrolling in a novel Complete Stack Developer – MERN Stack Grasp’s program. Get entire construction and checking out wisdom on the newest applied sciences via choosing the MERN Stack Developer Direction. Touch us TODAY!
Conclusion
In C, Linear Seek comes to traversing an inventory or array sequentially to look if an access is there. The purpose is to start traversing the array and examine pieces of the array one after the other, beginning with the primary part, till a fit is found out or the array’s finish is reached.
We are hoping this text helped you achieve wisdom of the C program for Linear Seek. On this article, we mentioned the makes use of of a Linear Seek, time and area complexity, and solution to put in force Linear Seek in a code. We additionally discovered how we will be able to use it in our device construction initiatives.
To grasp extra concerning the Linear Seek in C Program, you’ll be able to join within the Complete Stack Developer – MERN Stack presented via Simplilearn in collaboration with Caltech CTME. This Internet Construction direction is a descriptive on-line bootcamp that incorporates 25 initiatives, a capstone undertaking, and interactive on-line categories. Along with Linear Seek in C Program and different comparable ideas, the direction additionally main points the whole lot you want to change into a full-stack technologist and boost up your profession as a device developer.
Simplilearn additionally gives loose on-line skill-up classes in numerous domain names, from information science and trade analytics to device construction, AI, and system finding out. You’ll absorb any of those loose classes to improve your talents and advance your profession.
supply: www.simplilearn.com
