Kruskal Set of rules: Evaluate & Create Minimal Spanning Tree

What Is Kruskal Set of rules?

Kruskal’s Set of rules is a vintage set of rules utilized in graph concept to search out the Minimal Spanning Tree (MST) of a attached, undirected graph. The MST is a subset of the sides that connects the entire vertices with none cycles and with the minimal imaginable general edge weight. Kruskal’s Set of rules is grasping, which means it builds the MST via at all times opting for the following shortest edge that does not shape a cycle.

Steps of Kruskal’s Set of rules

1. Kind All Edges: Start via sorting the entire edges within the graph in a non-decreasing order in their weight.
2. Initialize Subsets: Create a suite for each and every vertex within the graph. That is in most cases finished the use of a Disjoint Set Union (DSU) or Union-To find knowledge construction, which is helping in managing and merging units successfully.
3. Iterate Over Looked after Edges: Traverse the taken care of edge listing and for each and every edge, resolve if including it to the rising spanning tree would shape a cycle. That is finished via checking if the 2 vertices of the threshold belong to other units. In the event that they do, come with this edge within the MST and union the units of those two vertices. In the event that they belong to the similar set, together with this edge would shape a cycle, so it’s discarded.
4. Repeat Till MST is Whole: Proceed the method till there are V−1 edges within the MST, the place V is the choice of vertices within the graph.

Need a Best Tool Building Process? Get started Right here!

Complete Stack Developer – MERN StackDiscover Program

What Is a Spanning Tree?

A spanning tree is a subset of a graph that comes with the entire graph’s vertices and one of the vital edges of the unique graph, aspiring to don’t have any cycles. A spanning tree isn’t essentially distinctive – it’s imaginable for there to be more than one spanning timber for a given graph. On the other hand, a given graph will at all times have no less than one spanning tree. The perimeters in a spanning tree are referred to as “department edges,” whilst the sides no longer within the spanning tree are referred to as “cycle edges.” And this sort of graph is helping discover the minimal choice of edges required to glue all vertices in a graph. It is usually used to create minimally secured networks with redundant paths.

What Is a Minimal Spanning Tree? 

A minimal spanning tree (MST) is a subset of the sides of a attached, edge-weighted graph that connects the entire vertices in combination with none cycles and with the minimal imaginable general edge weight. This can be a method of discovering probably the most economical technique to attach a suite of vertices. A minimal spanning tree isn’t essentially distinctive. All of the weights of the sides within the MST will have to be distinct. If the entire weights of the sides within the graph are the similar, then any spanning tree of the graph is an MST. The perimeters of the minimal spanning tree will also be discovered the use of the grasping set of rules or the extra refined Kruskal or Prim’s set of rules.

Get Mentored via Main Java Mavens!

Complete Stack Java DeveloperDiscover Program

How Many Edges Does a Minimal Spanning Tree Have? 

A minimal spanning tree (MST) is a subset of the sides of a attached, undirected graph that connects the entire vertices with probably the most negligible imaginable general weight of the sides. A minimal spanning tree has exactly n-1 edges, the place n is the choice of vertices within the graph. 

Growing Minimal Spanning Tree The usage of Kruskal Set of rules

You are going to first glance into the stairs concerned with Kruskal’s Set of rules to generate a minimal spanning tree:

• Step 1: Kind all edges in expanding order in their edge weights.
• Step 2: Select the smallest edge.
• Step 3: Test if the brand new edge creates a cycle or loop in a spanning tree.
• Step 4: If it doesn’t shape the cycle, then come with that edge in MST. Another way, discard it.
• Step 5: Repeat from step 2 till it comprises |V| – 1 edges in MST.

The usage of the stairs stated above, you’ll generate a minimal spanning tree construction. So, now take a look at an instance to know this procedure higher.

The graph G(V, E) given under comprises 6 vertices and 12 edges. And you’ll create a minimal spanning tree T(V’, E’) for G(V, E) such that the choice of vertices in T shall be 6 and edges shall be 5 (6-1).

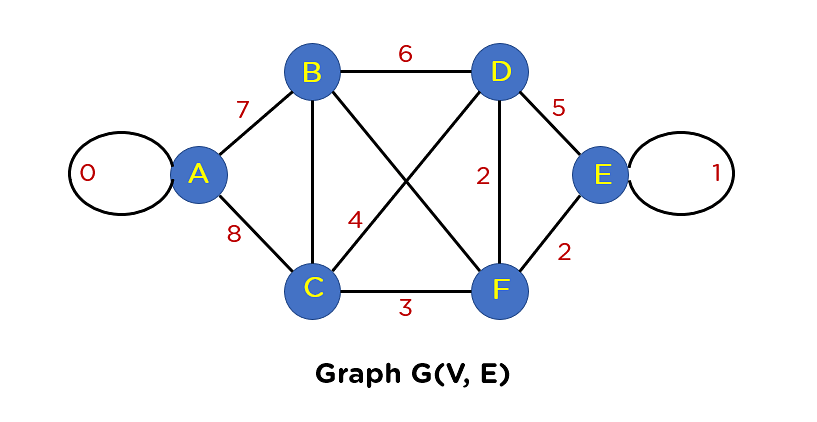
In case you follow this graph, you’ll discover two looping edges connecting the similar node to itself once more. And you already know that the tree construction can by no means come with a loop or parallel edge. Therefore, essentially it is very important take away those edges from the graph construction.

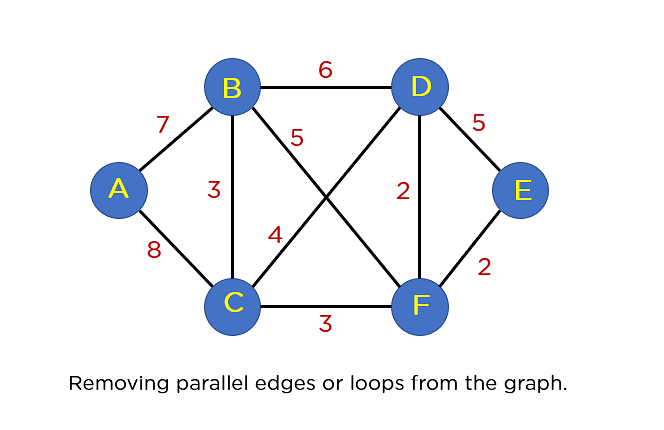
The next move that you’re going to continue with is arranging all edges in a taken care of listing via their edge weights.

After this step, you’ll come with edges within the MST such that the incorporated edge would no longer shape a cycle on your tree construction. The primary edge that you’re going to select is edge EF, because it has a minimal edge weight this is 2.

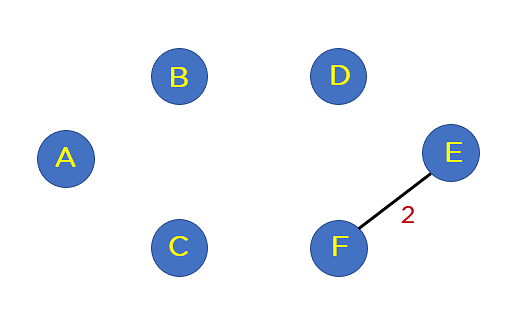
Upload edge FD to the spanning tree.

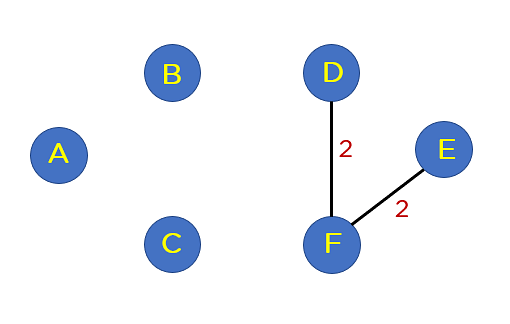
Upload edge BC and edge CF to the spanning tree because it does no longer generate any loop.

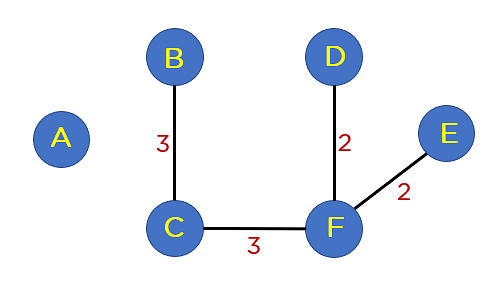
Subsequent up is edge CD. This edge generates the loop in Your tree construction. Thus, you’ll discard this edge.

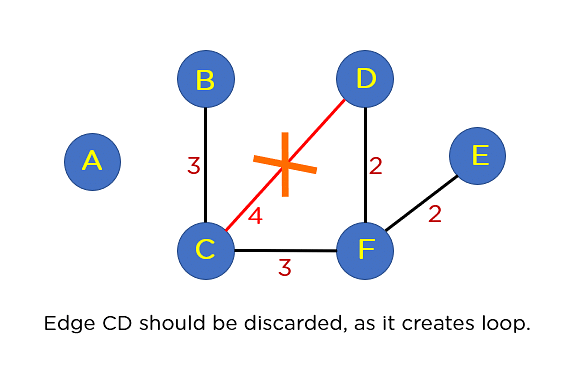
Following edge CD, you could have edge BF. This edge additionally creates the loop; therefore you’ll discard it.

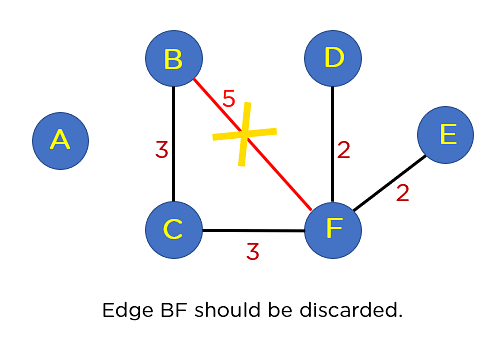
Subsequent up is edge BD. This edge additionally formulates a loop, so you’ll discard it as neatly.

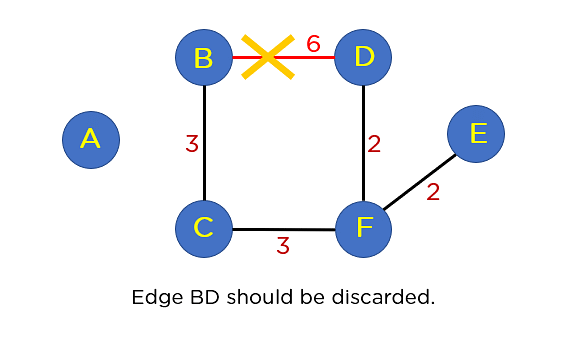
Subsequent to your taken care of listing is edge AB. This edge does no longer generate any cycle, so you want no longer come with it within the MST construction. By way of together with this node, it is going to come with 5 edges within the MST, so that you don’t must traverse any more within the taken care of listing. The general construction of your MST is represented within the symbol under:

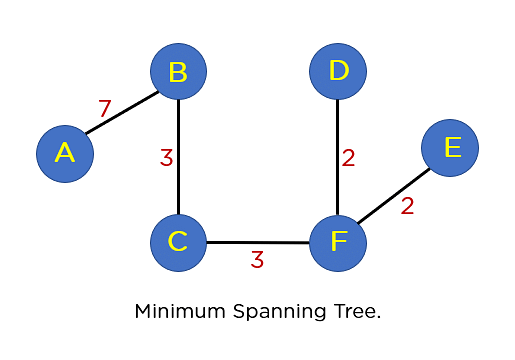
The summation of the entire edge weights in MST T(V’, E’) is the same as 17, which is the least imaginable edge weight for any imaginable spanning tree construction for this actual graph. Transferring forward, you’ll know about imposing Kruskal algorithms the use of the Union To find Set of rules.

Need a Best Tool Building Process? Get started Right here!

Complete Stack Developer – MERN StackDiscover Program

What Is Union To find Set of rules?

Union To find is an set of rules that assists in keeping observe of parts which are break up into one or over one disjoint set. It has two number one operations: To find and Union. The To find operation returns the set of parts to which the given component (argument) belongs, while the Union operation merges two disjoint units.

You wish to have to divide the equipped graph G(V, E) into 3 separate units whilst construction the Minimal Spanning Tree the use of Kruskal’s method. The primary comprises edge weight values, the second one has a tree hierarchy for distinct nodes, and the 3rd comprises the rank of all nodes. By way of the use of Union and To find operations, it joins the distinct nodes, which might be handled as other timber themselves, to formulate a minimal spanning tree.

Implementation of Kruskal Set of rules in C

Any MST set of rules revolves round figuring out whether or not including an edge would lead to a loop or no longer. Union To find is the preferred set of rules for figuring out this. The Union-To find set of rules separates vertices into clusters, permitting you to resolve whether or not two vertices belong to the similar cluster and therefore if including an edge will produce a cycle.

The option to enforce the Kruskal set of rules the use of Union-To find is given under:

• Assemble a construction to stay observe of the supply and vacation spot nodes, in addition to their weight.
• Kind the entire edges of a graph in keeping with their edge-weight values.
• Create 3 distinct units to handle nodes of a graph, their hierarchy in a tree, and corresponding ranks for each node.
• Essentially, initialize all rank values to 0 and father or mother values to -1 (representing each and every node as its personal tree itself).
• For each and every insertion of an edge in MST, you’ll replace the rank and father or mother of each and every node.
• Don’t insert the threshold connecting two nodes if they’ve the similar father or mother node, as this may increasingly purpose a cycle within the tree construction.

Now, you’ll perceive this implementation technique with the assistance of an instance. The graph for which you’ll broaden a minimal spanning tree the use of Kruskal’s method is given under:

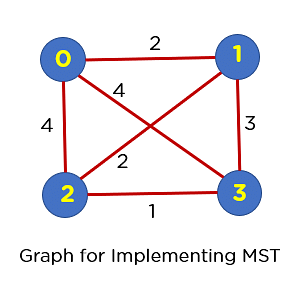
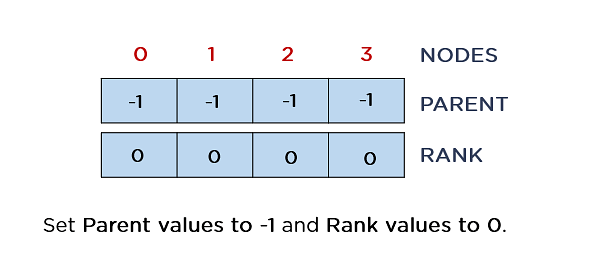
First of all, it is very important create two units for keeping up father or mother price and rank price for each and every node. In conjunction with that, you’ll create a construction to stay the sides of the graph. For the entire nodes within the graph, you’ll initialize father or mother values to -1 and rank values to 0. The rationale in the back of this is that you want to regard the entire nodes of a graph as timber themselves.

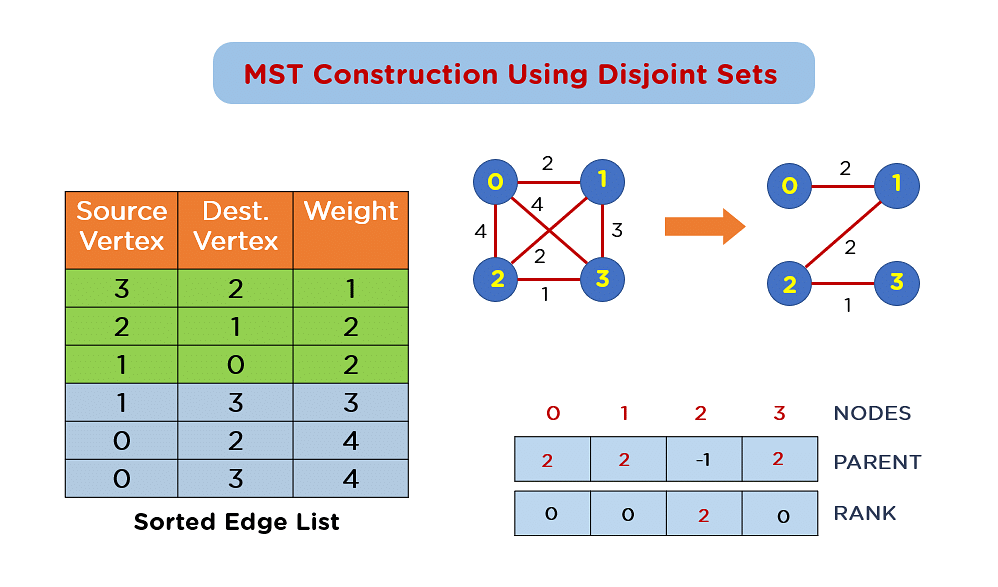
Moreover, remember the fact that on every occasion you sign up for two disjoint tree constructions in combination, the rank of 1 being pointed to will build up via one. So, whenever you upload edges into the MST, the rank and father or mother values of incorporated nodes will alternate. This actual graph will display the state of units, just like the determine under.

The C program to enforce Kruskal’s set of rules the use of above-mentioned technique is as follows:

#come with <stdlib.h>
#come with <string.h>
#come with <stdio.h>
//construction that denotes a weighted edge
struct Edge
{
int supply, vacation spot, weight;
};
//construction that denotes a weighted, undirected and attached graph
struct Graph
{
int Node, E;struct Edge* edge;
};
//allocates reminiscence for storing graph with V vertices and E edges
struct Graph* GenerateGraph(int Node, int E)
{
struct Graph* graph = (struct Graph*)(malloc(sizeof(struct Graph
)));
graph->Node = Node;
graph->E = E;
graph->edge = (struct Edge*)malloc(sizeof( struct Edge));
go back graph;
}
//subset for Union-To find
struct tree_maintainance_set {int father or mother;int rank;};
//reveals the set of selected component i the use of direction compression
int find_DisjointSet(struct tree_maintainance_set subsets[], int I)
{
//discover root and make root as father or mother of i
if (subsets[i].father or mother != i)
subsets[i].father or mother= find_DisjointSet(subsets, subsets[i].father or mother);go back subsets[i].father or mother;
}
//Creates the Union of 2 units
void Union_DisjointSet(struct tree_maintainance_set subsets[], int x, int y){int xroot = find_DisjointSet(subsets, x);int yroot = find_DisjointSet(subsets, y);
//connecting tree with lowest rank to the tree with best possible rank
if (subsets[xroot].rank < subsets[yroot].rank)subsets[xroot].father or mother = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)subsets[yroot].father or mother = xroot;
//if ranks are similar, arbitrarily build up the rank of 1 node
else{subsets[yroot].father or mother = xroot;subsets[xroot].rank++;}}
//serve as to match edges the use of qsort() in C programming
int myComp(const void* a, const void* b)
{
struct Edge* a1 = (struct Edge*)a;
struct Edge* b1 = (struct Edge*)b;
go back a1->weight > b1->weight;
}
//serve as to build MST the use of Kruskal’s method
void KruskalMST(struct Graph* graph)
{int Node = graph->Node;
struct Edgeresult[Node]; 
int e = 0; int i = 0;      
//sorting all edges
qsort(graph->edge, graph->E, sizeof(graph->edge[0]),myComp);
//reminiscence allocation for V subsets
struct tree_maintainance_set* subsets= (struct tree_maintainance_set*)malloc(Node * sizeof(struct tree_maintainance_set));
//V subsets containing just one component
for (int v = 0; v < Node; ++v) {subsets[v].father or mother = v;subsets[v].rank = 0;}
//Edge traversal restrict: V-1
whilst (e < Node - 1 && i < graph->E)
{struct Edge next_edge = graph->edge[i++];
int x = find_DisjointSet(subsets, next_edge.supply);
int y = find_DisjointSet(subsets, next_edge.vacation spot);
if (x != y) 
{consequence[e++] = next_edge;
Union_DisjointSet(subsets, x, y);}
}
//printing MST
printf("Edges created in MST are as under: n");
int minimumCost = 0;
for (i = 0; i < e; ++i)
{
printf("%d -- %d == %dn", consequence[i].supply,consequence[i].vacation spot, consequence[i].weight);minimumCost += consequence[i].weight;
}
printf("The Price for created MST is : %d",minimumCost);
go back;
}
int major()
{
int Node = 4;
int E = 6;
struct Graph* graph = GenerateGraph(Node, E);
//Growing graph with handbook price insertion
// upload edge 0-1
graph->edge[0].supply = 0;
graph->edge[0].vacation spot = 1;
graph->edge[0].weight = 2;}
// upload edge 0-2
graph->edge[1].supply = 0;
graph->edge[1].vacation spot = 2;
graph->edge[1].weight = 4;
// upload edge 0-3
graph->edge[2].supply = 0;
graph->edge[2].vacation spot = 3;
graph->edge[2].weight = 4;
// upload edge 1-3
graph->edge[3].supply = 1;
graph->edge[3].vacation spot = 3;
graph->edge[3].weight = 3;
// upload edge 2-3
graph->edge[4].supply = 2;
graph->edge[4].vacation spot = 3;
graph->edge[4].weight = 1;
// upload edge 1-2
graph->edge[5].supply = 1;
graph->edge[5].vacation spot = 2;
graph->edge[5].weight = 2;
KruskalMST(graph);
go back 0;
}

Output:

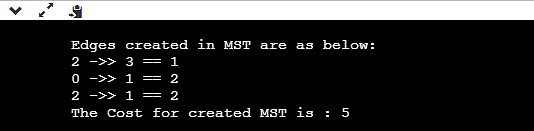
You’ll check this output’s accuracy via evaluating it with the MST construction proven above. The full charge for this MST is 5.

Get the Coding Talents You Want to Be successful

Complete Stack Developer – MERN StackDiscover Program

Implementation of Kruskal Set of rules in C++

#come with <iostream>
#come with <vector>
#come with <set of rules>

the use of namespace std;

// Outline an edge construction
struct Edge {
    int src, dest, weight;
};

// A category to constitute a graph
magnificence Graph {
public:
    int V, E; // V -> choice of vertices, E -> choice of edges
    vector<Edge> edges; // number of all edges

    Graph(int V, int E);
    void addEdge(int u, int v, int w);
    int discover(vector<int>& father or mother, int i);
    void Union(vector<int>& father or mother, vector<int>& rank, int x, int y);
    void kruskalMST();
};

// Constructor
Graph::Graph(int V, int E) {
    this->V = V;
    this->E = E;
    edges.resize(E);
}

// Serve as so as to add an edge to the graph
void Graph::addEdge(int u, int v, int w) {
    Edge edge = {u, v, w};
    edges.push_back(edge);
}

// A application serve as to search out set of a component i (makes use of direction compression methodology)
int Graph::discover(vector<int>& father or mother, int i) {
    if (father or mother[i] != i) {
        father or mother[i] = discover(father or mother, father or mother[i]);
    }
    go back father or mother[i];
}

// A serve as that does union of 2 units of x and y (makes use of union via rank)
void Graph::Union(vector<int>& father or mother, vector<int>& rank, int x, int y) {
    int xroot = discover(father or mother, x);
    int yroot = discover(father or mother, y);

    if (rank[xroot] < rank[yroot]) {
        father or mother[xroot] = yroot;
    } else if (rank[xroot] > rank[yroot]) {
        father or mother[yroot] = xroot;
    } else {
        father or mother[yroot] = xroot;
        rank[xroot]++;
    }
}

// The principle serve as to build MST the use of Kruskal's set of rules
void Graph::kruskalMST() {
    vector<Edge> consequence; // Retailer the ensuing MST
    int e = 0; // An index variable, used for consequence[]
    int i = 0; // An index variable, used for taken care of edges

    // Step 1: Kind the entire edges in non-decreasing order in their weight.
    kind(edges.start(), edges.finish(), [](Edge a, Edge b) {
        go back a.weight < b.weight;
    });

    // Allocate reminiscence for growing V subsets
    vector<int> father or mother(V);
    vector<int> rank(V, 0);

    // Create V subsets with unmarried parts
    for (int v = 0; v < V; ++v) {
        father or mother[v] = v;
    }

    // Collection of edges to be taken is the same as V-1
    whilst (e < V - 1 && i < edges.measurement()) {
        // Step 2: Select the smallest edge. And increment the index for subsequent iteration
        Edge next_edge = edges[i++];

        int x = discover(father or mother, next_edge.src);
        int y = discover(father or mother, next_edge.dest);

        // If together with this edge does no longer purpose a cycle, come with it in consequence
        // and increment the index of consequence for subsequent edge
        if (x != y) {
            consequence.push_back(next_edge);
            Union(father or mother, rank, x, y);
            e++;
        }
        // Another way discard the next_edge
    }

    // Print the ensuing MST
    cout << "Following are the sides within the built MSTn";
    for (const auto& edge : consequence) {
        cout << edge.src << " -- " << edge.dest << " == " << edge.weight << endl;
    }
}

int major() {
    int V = 4; // Collection of vertices in graph
    int E = 5; // Collection of edges in graph
    Graph graph(V, E);

    // Upload edges
    graph.addEdge(0, 1, 10);
    graph.addEdge(0, 2, 6);
    graph.addEdge(0, 3, 5);
    graph.addEdge(1, 3, 15);
    graph.addEdge(2, 3, 4);

    // Serve as name
    graph.kruskalMST();

    go back 0;
}

Clarification

1. Edge Construction: Defines an edge with supply (src), vacation spot (dest), and weight (weight).
2. Graph Magnificence: Accommodates vertices (V), edges (E), and a number of edges (edges). Purposes so as to add edges, discover the set of a component, union of 2 units, and the primary serve as to compute the MST (kruskalMST).
3. addEdge: Provides an edge to the graph.
4. discover: Unearths the consultant (root) of the set that component i is a part of, with direction compression to hurry up long term queries.
5. Union: Unites two units (x and y), the use of union via rank to stay the tree flat.
6. kruskalMST: Types the sides via weight; Makes use of a union-find construction to control disjoint units; Iterates during the edges, including them to the MST if they do not shape a cycle, till the MST comprises V-1 edges.
7. Major Serve as: Creates a graph, provides edges, and calls kruskalMST to search out and print the MST.

This is Learn how to Land a Best Tool Developer Process

Complete Stack Developer – MERN StackDiscover Program

Implementation of Kruskal Set of rules in Python

Step 1: Outline the Union-To find (Disjoint Set) Information Construction

magnificence DisjointSet:
    def __init__(self, vertices):
        self.father or mother = {v: v for v in vertices}
        self.rank = {v: 0 for v in vertices}
    
    def discover(self, merchandise):
        if self.father or mother[item] == merchandise:
            go back merchandise
        else:
            self.father or mother[item] = self.discover(self.father or mother[item])
            go back self.father or mother[item]
    
    def union(self, set1, set2):
        root1 = self.discover(set1)
        root2 = self.discover(set2)
        
        if root1 != root2:
            if self.rank[root1] > self.rank[root2]:
                self.father or mother[root2] = root1
            elif self.rank[root1] < self.rank[root2]:
                self.father or mother[root1] = root2
            else:
                self.father or mother[root2] = root1
                self.rank[root1] += 1

Step 2: Outline the Kruskal’s Set of rules

def kruskal(vertices, edges):
    # Kind edges via weight
    edges = taken care of(edges, key=lambda edge: edge[2])
    
    # Initialize Disjoint Set
    disjoint_set = DisjointSet(vertices)
    
    mst = []
    
    for edge in edges:
        u, v, weight = edge
        # Test if together with this edge would shape a cycle
        if disjoint_set.discover(u) != disjoint_set.discover(v):
            disjoint_set.union(u, v)
            mst.append(edge)
    
    go back mst

Step 3: Instance Utilization

# Record of vertices within the graph
vertices = ['A', 'B', 'C', 'D', 'E']

# Record of edges within the graph (u, v, weight)
edges = [
    ('A', 'B', 1),
    ('A', 'C', 3),
    ('B', 'C', 3),
    ('B', 'D', 6),
    ('C', 'D', 4),
    ('C', 'E', 2),
    ('D', 'E', 5)
]

# Compute the Minimal Spanning Tree the use of Kruskal's Set of rules
mst = kruskal(vertices, edges)

# Print the outcome
print("Edges within the Minimal Spanning Tree:")
for edge in mst:
    print(edge)

Clarification

1. Disjoint Set Magnificence: Initialization: Creates a father or mother pointer and rank for each and every vertex; To find Operation: Implements direction compression to search out the basis of a suite; Union Operation: Makes use of union via rank to glue smaller intensity timber beneath the basis of deeper timber.
2. Kruskal’s Set of rules: Sorting Edges: Types the sides according to their weights in ascending order; Initialization of Disjoint Set: Creates disjoint units for each and every vertex; Edge Variety: Iterates during the taken care of edges and comprises an edge within the MST if it doesn’t shape a cycle; Returning MST: The MST is returned as an inventory of edges.
3. Instance Utilization: Defines vertices and edges; Calls the Kruskal serve as and prints the MST edges.

Dive Deep into Core Python Ideas

Python Certification PathENROLL NOW

Implementation of Kruskal Set of rules in Java

import java.util.*;

magnificence Edge implements Similar<Edge> {
    int src, dest, weight;

    // Comparator serve as used for sorting edges according to their weight
    public int compareTo(Edge compareEdge) {
        go back this.weight - compareEdge.weight;
    }
};

magnificence Subset {
    int father or mother, rank;
};

magnificence Graph {
    int V, E; // Collection of vertices and edges
    Edge[] edges; // Number of all edges

    Graph(int v, int e) {
        V = v;
        E = e;
        edges = new Edge[E];
        for (int i = 0; i < e; ++i) {
            edges[i] = new Edge();
        }
    }

    // A application serve as to search out the set of a component i (makes use of direction compression)
    int discover(Subset[] subsets, int i) {
        if (subsets[i].father or mother != i)
            subsets[i].father or mother = discover(subsets, subsets[i].father or mother);
        go back subsets[i].father or mother;
    }

    // A serve as that does union of 2 units of x and y (makes use of union via rank)
    void union(Subset[] subsets, int x, int y) {
        int xroot = discover(subsets, x);
        int yroot = discover(subsets, y);

        // Connect smaller rank tree beneath root of top rank tree
        if (subsets[xroot].rank < subsets[yroot].rank)
            subsets[xroot].father or mother = yroot;
        else if (subsets[xroot].rank > subsets[yroot].rank)
            subsets[yroot].father or mother = xroot;
        else {
            subsets[yroot].father or mother = xroot;
            subsets[xroot].rank++;
        }
    }

    // The principle serve as to build MST the use of Kruskal's set of rules
    void kruskalMST() {
        Edge[] consequence = new Edge[V]; // This may retailer the ensuing MST
        int e = 0; // An index variable, used for consequence[]
        int i = 0; // An index variable, used for taken care of edges
        for (i = 0; i < V; ++i)
            consequence[i] = new Edge();

        // Step 1: Kind the entire edges in non-decreasing order in their weight.
        Arrays.kind(edges);

        // Allocate reminiscence for growing V subsets
        Subset[] subsets = new Subset[V];
        for (i = 0; i < V; ++i)
            subsets[i] = new Subset();

        // Create V subsets with unmarried parts
        for (int v = 0; v < V; ++v) {
            subsets[v].father or mother = v;
            subsets[v].rank = 0;
        }

        i = 0; // Index used to select the smallest edge

        // Collection of edges to be taken is the same as V-1
        whilst (e < V - 1) {
            // Step 2: Select the smallest edge. And increment the index for subsequent iteration
            Edge nextEdge = edges[i++];

            int x = discover(subsets, nextEdge.src);
            int y = discover(subsets, nextEdge.dest);

            // If together with this edge does no longer purpose a cycle, come with it in consequence
            // and increment the index of consequence for subsequent edge
            if (x != y) {
                consequence[e++] = nextEdge;
                union(subsets, x, y);
            }
            // Else discard the nextEdge
        }

        // Print the contents of consequence[] to show the constructed MST
        Machine.out.println("Following are the sides within the built MST:");
        for (i = 0; i < e; ++i)
            Machine.out.println(consequence[i].src + " -- " + consequence[i].dest + " == " + consequence[i].weight);
    }
}

public magnificence Kruskal {
    public static void major(String[] args) {
        int V = 4; // Collection of vertices within the graph
        int E = 5; // Collection of edges within the graph
        Graph graph = new Graph(V, E);

        // upload edge 0-1
        graph.edges[0].src = 0;
        graph.edges[0].dest = 1;
        graph.edges[0].weight = 10;

        // upload edge 0-2
        graph.edges[1].src = 0;
        graph.edges[1].dest = 2;
        graph.edges[1].weight = 6;

        // upload edge 0-3
        graph.edges[2].src = 0;
        graph.edges[2].dest = 3;
        graph.edges[2].weight = 5;

        // upload edge 1-3
        graph.edges[3].src = 1;
        graph.edges[3].dest = 3;
        graph.edges[3].weight = 15;

        // upload edge 2-3
        graph.edges[4].src = 2;
        graph.edges[4].dest = 3;
        graph.edges[4].weight = 4;

        graph.kruskalMST();
    }
}

Clarification

1. Edge Magnificence: This magnificence represents an edge with supply, vacation spot, and weight. It’s related to sorting edges via weight.

2. Subset Magnificence: Represents a subset for union-find.

3. Graph Magnificence: Accommodates strategies for locating the MST the use of Kruskal’s set of rules.

• discover(): Makes use of direction compression.
• union(): Makes use of union via rank.
• kruskalMST(): Major solution to carry out Kruskal’s set of rules.

4. Major Way: Initializes the graph, provides edges, and calls kruskalMST().

Get Mentored via Main Java Mavens!

Complete Stack Java DeveloperDiscover Program

Kruskal’s vs Prim’s Set of rules

Kruskal’s Set of rules

Kruskal’s grasping set of rules reveals a minimal spanning tree for a weighted, undirected graph. The set of rules begins with a wooded area consisting of the person nodes of the graph after which reveals the most affordable edge from each and every node and provides it to the wooded area. This procedure is repeated till just one tree is within the wooded area, the minimal spanning tree.

Kruskal’s set of rules is a minimal spanning tree set of rules that takes a graph as enter and reveals the subset of the sides of that graph. This enter paperwork a tree that comes with each vertex, the place the whole weight of the entire edges within the tree is minimized. The set of rules works via sorting the graph’s edges via weight, then taking the threshold with the bottom weight from the graph and including it to the tree. This procedure repeats till the entire vertices are incorporated within the tree.

Prim’s Set of rules

Prim’s set of rules could also be grasping and reveals a minimal spanning tree for a weighted undirected graph. On the other hand, the set of rules begins with a unmarried node after which provides the most affordable edge from that node to the tree. However Prim’s set of rules works otherwise than Kruskal’s set of rules. And this procedure is repeated till there are n-1 edges within the tree, the place n is the choice of nodes within the graph.

Kruskal’s Set of rules Complexity

Kruskal’s set of rules is a well known set of rules for locating the minimal spanning tree of a graph. This can be a grasping set of rules that uses the truth that the sides of a minimal spanning tree will have to shape a subset of the sides of every other spanning tree.

The time complexity of Kruskal’s Set of rules is O(ElogE), the place E is the choice of edges within the graph. This complexity is for the reason that set of rules makes use of a concern queue with a time complexity of O(logE). On the other hand, the distance complexity of the set of rules is O(E), which is slightly top.

Kruskal’s Set of rules Programs

Kruskal’s set of rules is common in pc science for locating the minimal spanning tree in a graph. A grasping set of rules selects the most affordable edge that doesn’t shape a cycle within the graph. The next are one of the vital packages of Kruskal’s set of rules:

• Community Design: Kruskal’s set of rules can be utilized to design networks with the least charge. It may be used to search out the least pricey community connections that may attach the entire nodes within the community.
• Approximation Algorithms: Kruskal’s set of rules can be utilized to search out approximate answers to a number of advanced optimization issues. It might probably additionally remedy the touring salesman downside, the knapsack downside, and different NP-hard optimization issues.
• Symbol Segmentation: Symbol segmentation is the method of partitioning a picture into more than one segments. Kruskal’s set of rules can be utilized to damage down a picture into its constituent portions in an effective method.
• Clustering: Clustering is the method of grouping knowledge issues according to their similarity.

Unharness Your Occupation as a Complete Stack Developer!

Complete Stack Developer – MERN StackEXPLORE COURSE

Conclusion

Mastering Kruskal’s Set of rules opens doorways to figuring out basic ideas in graph concept and tackling real-world issues successfully. From community design to clustering in gadget finding out, this set of rules’s packages are huge and impactful. By way of finding out Kruskal’s Set of rules from scratch, you might be laying a robust basis for extra complex subjects in pc science.

In a position to take your abilities to the following degree? Sign up in Simplilearn’s Complete Stack Developer – MERN Stack direction. Achieve complete wisdom and hands-on revel in in full-stack building, equipping you with the experience to excel within the tech business. Sign up for now and get started your adventure to changing into a talented developer!

FAQs

1. What Is the Good judgment of Kruskal Set of rules?

Kruskal’s Set of rules reveals the Minimal Spanning Tree (MST) of a attached, undirected graph via iteratively settling on the shortest edge that doesn’t shape a cycle. It begins via sorting all edges via weight after which makes use of a union-find knowledge construction to successfully test and merge disjoint units of vertices, making sure no cycles are shaped. The method continues till the MST comprises V−1 edges, the place V is the choice of vertices.

2. What Are the Benefits of Kruskal’s Set of rules?

Kruskal’s Set of rules has a number of benefits:

• It’s easy to know and enforce.
• It really works neatly with sparse graphs because it makes a speciality of edges quite than vertices.
• The set of rules can deal with disconnected parts and discover the MST for each and every attached part.
• It makes use of environment friendly knowledge constructions like union-find for cycle detection, making it computationally environment friendly with the time complexity of O(ElogE).

3. What Is the Distinction Between Dijkstra and Kruskal Set of rules?

Dijkstra’s Set of rules reveals the shortest direction from a unmarried supply to all different vertices in a weighted graph, specializing in vertex distances. It makes use of a concern queue to discover the closest vertex first. Against this, Kruskal’s Set of rules reveals the Minimal Spanning Tree (MST) for all of the graph via settling on edges in ascending order of weight, specializing in edges and the use of union-find to forestall cycles. Dijkstra’s is used for shortest-path issues, whilst Kruskal’s is used for MST issues.

4. The place Is Kruskal Set of rules Utilized in Actual Existence?

Kruskal’s Set of rules is utilized in community design, reminiscent of developing least-cost networks like telecommunications, electric grids, and pc networks. It is usually utilized in clustering algorithms in gadget finding out, symbol segmentation in pc imaginative and prescient, and more than a few optimization issues the place a minimal spanning tree is needed. Its skill to successfully arrange and attach parts with minimum general weight makes it precious in numerous fields reminiscent of transportation, logistics, and useful resource control.